Cuestionarios y Juegos didácticos

Las ecuaciones suelen clasificarse según el tipo de operaciones necesarias para definirlas y según el conjunto de números sobre el que se busca la solución. Entre los tipos más comunes están:

• Ecuaciones algebraicas
  • De primer grado o lineales
  • De segundo grado o cuadráticas
  • De tercer grado o cúbicas
  • Diofánticas o diofantinas: son aquellas cuya solución solo puede ser un número entero, es decir, en este caso A ⊆ ℤ.
  • Racionales, aquellas en las que uno o ambos miembros se expresan como un cociente de polinomios
• Ecuaciones trascendentes, cuando involucran funciones no polinómicas, como las funciones trigonométricas, exponenciales, logarítmicas, etc.

Resolución de ecuaciones

Resolver una ecuación es encontrar su dominio solución, que es el conjunto de valores de las incógnitas para los cuales la igualdad se cumple.

Por lo general, los problemas matemáticos pueden expresarse en forma de una o más ecuaciones, sin embargo no todas las ecuaciones tienen solución, ya que es posible que no exista ningún valor de la incógnita que haga cierta una igualdad dada. En ese caso, el conjunto de soluciones de la ecuación será vacío y se dice que la ecuación no es resoluble. De igual modo, puede tener un único valor, o varios, o incluso infinitos valores, siendo cada uno de ellos una solución particular de la ecuación.

Si cualquier valor de la incógnita hace cumplir la igualdad (esto es, no existe ningún valor para el cual no se cumpla) la ecuación es en realidad una identidad.

Funciones:

Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda, llamada imagen. Siendo x el tiempo en minutos que dura el viaje. Como podemos observar la función relaciona dos variables. x e y.

En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio ) y otro conjunto de elementos Y (llamado codominio ) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).

Trigonometría:

La trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Razones trigonométricas en triángulos rectángulos:

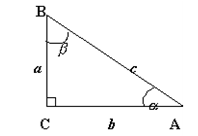
Teorema : En todo triángulo  rectángulo se cumple que:

• Seno de un ángulo agudo equivale a la razón entre el cateto que se le opone y la hipotenusa. En símbolo: Si ABC es rectángulo entonces: sen a = a /c  y  sen b = b/c. 
• Coseno de un ángulo agudo equivale a la razón entre el cateto adyacente al ángulo y la hipotenusa. Es decir,  cos a = b/c y  cos b = a /c. 
• Tangente de un ángulo agudo equivale a la razón entre el cateto opuesto al ángulo y el cateto adyacente. Es decir, tan a = a /b y tan b = b/a. 
• Cotangente de un ángulo agudo equivale a la razón entre el cateto adyacente al ángulo y el cateto opuesto. Es decir, cot a = b/a  y  co tb = a /b. 

Nota :  Las  razones  trigonométricas  solo  son  aplicables  a  los  ángulos agudos del triángulo rectángulo.

Identidades Trigonométricas:

1. sen²x + cos²x = 1
2. sen²x = 1 – cos²x
3. cos²x = 1 – sen²x
4. sen2x = 2senx.cosx
5. cos2x = cos²x – sen²x
6. ta n x =  senx / cosx
7. cot x = cosx / senx
8. 1 + ta n²x = 1/cos²x
9. sen( x ± y )= senx.cosy ± cosx.seny
10. Cos( x ± y )= cosx.cosy ± senx.seny

Fórmulas de Reducción:

II cuadrante          III cuadrante      IV cuadrante

Siendo α el ángulo dado y x el ángulo del primer cuadrante que le corresponde.

Paridad de las funciones trigonométriicas conocidas:

1. sen(­x)= ­ senx
2. cos(­x)= cosx
3. ta n(­x)= ­ ta nx
4. cot(­x)= ­ cotx

Signos de las funciones por cuadrantes:

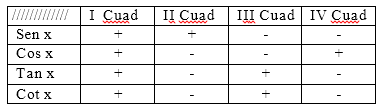
Tabla de valores Notables y Axiales:

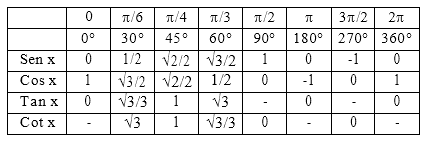
Geometría: